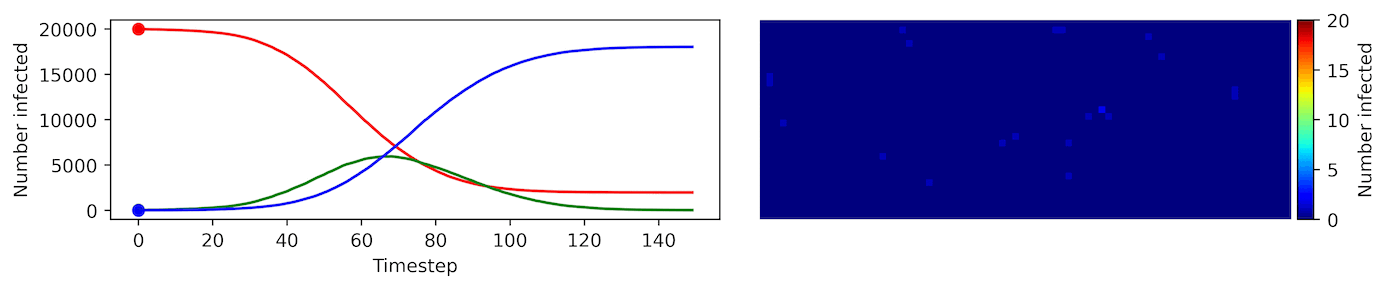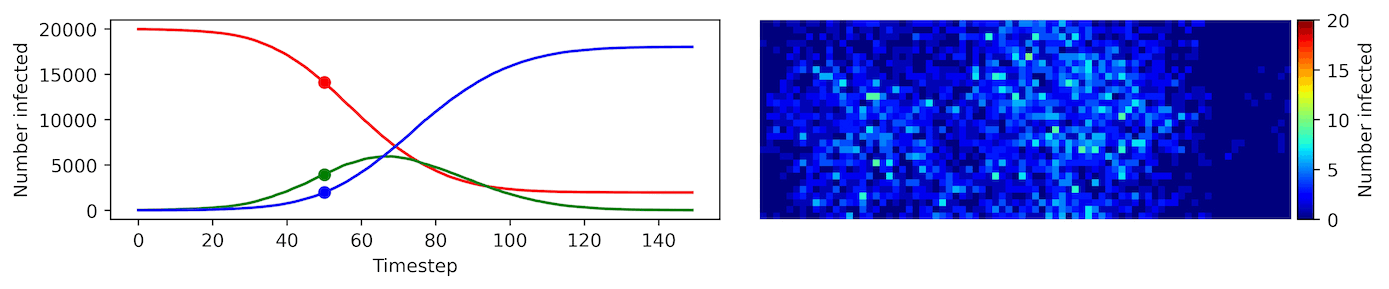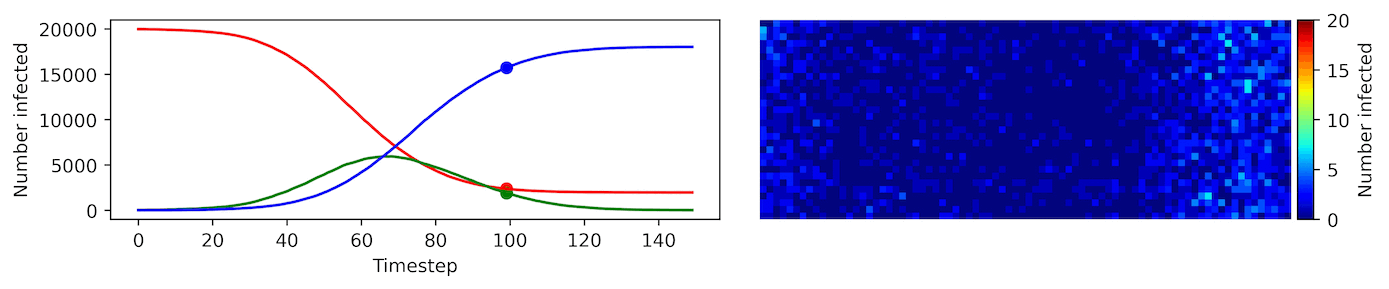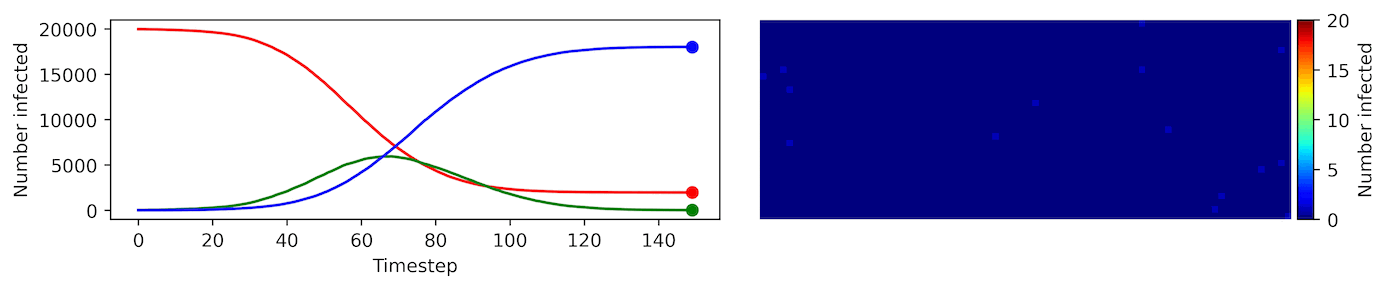
Image, text and audio are examples of structured multivariate data where we have a total or partial ordering over the entries of our data points and also may exhibit long-range structure extending over many pixels, words or seconds of speech. As a consequence, it is difficult to model these kinds of data using models that allow for only short-range structure such as HMMs or which can make use of only pairwise dependency structures such as the covariance matrix in a multivariate normal distribution. What if we’d like to build Bayesian models with more sophisticated structure?
There exists a tremendous number of applications in which we might like to quantify our uncertainty regarding missing portions of structured data so that we can understand what the missing completion might look like. For example, an X-ray of a fractured wrist may be partially occluded and we would like to know whether the rest of a partially observed crack is large or small, conditional on the parts of the X-ray that we can actually observe. Ideally, we would be presented with an entire distribution of image completions which exhibit completed structure in proportion to their conditional probability given the observed piece. I call this task posterior inpainting which is a mcore stringent definition of a task already explored somewhat in the literature as pluralistic image completion (Zheng et al., 2019) or probabilistic semantic inpainting (Dupont and Suresha, 2019). This problem is mathematically identical to that of super-resolution; if we consider observed pixels on a regular grid and assume that between every pair of observed pixels is a series of $M$ masked pixels then the observed pixels constitute a downsampled version of the entire image with a resolution equal to $1/M$ of the original. Colorization can also be placed within the same formalism except we treat some of the channels as missing data.
Posterior inpainting: problem setup & formalism
We designate $x$ to be a single observation which is itself a vector with elements $x_1, x_2,…x_D$. For image data, this amounts to describing $x$ as an image with $D$ pixels. Where necessary, we may refer to alternative observations in the larger dataset as $\mathcal{D}={ x^{(1)},x^{(2)},…,x^{(N)}}$. Under several popular generative models of structured data such as variational autoencoders (VAEs) and generative adversarial networks (GANs), it is also assumed each data point $x$ has a latent representation $z$ that encodes the information in $x$ in a compressed, low-dimensional format. Not all state-of-the-art generative models share this assumption, however! Autoregressive models such as PixelCNNs or PixelRNNs may work either with or without the usage of latent variables.
When latent variables are used, we often represent the function linking the latent code $z$ to the observed data $x$ as $f_\theta(z)$ with $\theta$ representing the parameters of the generative model $f$. In the case of $L_2$ pixelwise reconstruction error for image data, we could thus represent the likelihood for $x$ given $z$ as \(p_\theta(x\vert z)=MVN(f_\theta(z),\sigma^2_\epsilon I)\). This multivariate normal specification is simply saying that the log-likelihood has the form \(\propto \frac{1}{\sigma^2_\epsilon} \vert\vert x-f_\theta(z)\vert\vert_2^2\). Note that $f_\theta$ is a deterministic function (though we could relax this if we had a stochastic generative network such as a Bayesian neural net) so each latent $z$ is mapped to exactly one output image. In the event that we have a partially observed $\tilde{x}$ missing some of its pixels, there may be multiple $\tilde{z}^{(1)},\tilde{z}^{(2)},…,\tilde{z}^{(L)}$ which all yield some $f_\theta(\tilde{z})$ which is a good match for $x$. The central problem I’m addressing in this post is the sampling and computation related to obtaining these $\tilde{z}$ such that they are truly representative of the posterior distribution $p(\tilde{z} \vert \tilde{x})$. The next section is a review of papers which attempt to address this problem. Here’s a glossary of some of the terms that will be used frequently:
- $x$ indicates a single image with a partially observed counterpart $\tilde{x}$
- $z$ is the corresponding latent code for $x$ and $\tilde{z}$ is one of potentially many latent codes consistent with the partially observed $\tilde{x}$
- The generative model linking the latent code $z$ is denoted by $f_\theta$. For a variational autoencoder, this is the decoder network while for GANs, this is the generator. We refer to the weights of these networks as $\theta$.
- An estimator of $z$ is written as $\hat{z}$
- If a variational encoder network is used, $q_\phi(z\vert x)$ is used to refer to the conditional distribution of the latent code $z$ given image $x$. Note that this is conceptually quite different from a posterior $\propto p_\theta (x\vert z)p_\lambda(z)$ because the latter only requires a generative model $f_\theta$ and a prior on $z$ with parameters $\lambda$!
Review
Semantic image inpainting with deep generative models: Yeh et al. 2017
As soon as deep generative models such as VAEs and GANs started producing visually appealing samples when trained on more sophisticated data, researchers started investigating ways to use them to help solve a range of computer vision tasks including image inpainting. Yeh et al. 2017 presented a very straightforward and common-sense way to tackle image inpainting with a DGM. The basic recipe that they suggested for completing an image $\tilde{x}$ is:
- Pick a randomly initialized $\hat{z}_0$
- Calculate a loss function $L(\hat{z})=\gamma h(\hat{z}) +\vert\vert f_\theta(\hat{z}) - \tilde{x}\vert\vert$ where $\vert\vert \cdot \vert\vert$ denotes the norm or error function of your choice, $h$ is a prior loss and $\gamma$ is a weighting factor. This study used both $L_1$ and $L_2$ norms.
- Use a gradient descent optimization scheme to repeatedly apply the update \(\hat{z}_{t+1}=\hat{z}_t + \alpha\nabla_\hat{z}L(\hat{z}_{t})\) with some learning rate $\alpha$
- Since $\vert\vert f_\theta(\hat{z}) - \tilde{x}\vert\vert$ is likely going to be nonzero, apply image post-processing to blend together any sharp discontinuities between the completion $f_\theta(\hat{z})$ and the original image $\tilde{x}$.
While this procedure is guaranteed to converge to a local minimum, this paper doesn’t provide a recipe to either escape these minima or try to draw a range of samples. That’s beside the point, though, since the main contribution of this paper was simply to show how to get a single inpainted completion at all.
It’s a shame that the author’s didn’t report on any results with injected noise in step #3 above (e.g. using an update rule \(\hat{z}_{t+1}=\hat{z}_t + \alpha\nabla_\hat{z}L +\epsilon\) with $\epsilon$ drawn from an isotropic Gaussian) since this very nearly turns it into a Langevin sampler which I suspect would be a highly effective sampling scheme for this problem.
There’s an application paper by Dupont et al. 2018 which is nearly the exact same method used by Yeh et al. save with a minor modification to a mask applied to the loss function. As the authors of this paper noted:
To the best of our knowledge, creating models that can simultaneously (a) generate realistic images, (b) honor constraints, (c) exhibit high sample diversity is an open problem.
Clearly, the limitations of this approach are noted - getting high sample diversity could be challenging!
In an apparent follow-up to the challenge noted in the previous section, Dupont and Suresha
attempted to address the major shortcomings of the Dupont et al. (2018) approach by embracing a latent variable-free approach that allowed for straightforward sampling from conditional distributions over images. The basic idea in this paper is to augment a PixelCNN’s predictive distribution over pixels to include information which is outside of the usual raster scan ordering imposed on the sequence of pixels.
We can think of the basic PixelCNN with weights $\theta$ as an autoregressive generative model $f_\theta(x_i\vert x_1,…x_{i-1})$. The general problem that Dupont and Suresha tackle is how to augment the conditioning set of variables with pixels that might be out of raster scan order, yet still observed. Let’s denote the set of observed pixels as $X_c$. Then, the generative model becomes $f_\theta(x_i\vert {x_1,…,x_{i-1}}\cup X_c)$. To implement the PixelCNN constrained to match observations, the authors represent the conditional likelihood of the discretized categories of $x_i$ to be log-linear in two different networks: (1) a standard PixelCNN with little modification, and (2) a fairly standard ConvNet which takes in masked pixels and outputs a logit. The second network also needs to have an extra channel for its inputs to indicate which pixels are masked since, for example, a value of zero in the masked data could correspond to either missing data or an observed value of zero. This has an advantage over latent variable-based approaches in that the samples of the completed image $\hat{x}$ will not need Poisson blending to match the observed pixels - there is no generation of the already-observed pixels in this procedure
I have to say that I am really impressed with the quality and diversity of the samples drawn from the conditional distribution over completions - I think this is a front-runner and current SOTA for posterior image completion.
This paper was published in CVPR and either because of the journal’s format or because the study is heavy on technical details I found it to be very difficult to read. Unfortunately, I am unable to tell what the essence of this work is besides the fact that they pair two generative networks together which are trained on differing tasks. There were many details that would have ideally been given a longer treatment in this which likely contributed to it being relatively difficult to follow. This may have been an unavoidable consequence of the journal length format, however, and I do not intend this to be criticism of the authors’ writing.
A Bayesian perspective on the deep image prior: Cheng et al. 2019
The main contribution of this work is showing that sampled images from a deep generative model prior to training (AKA the deep image prior) are actually draws from a Gaussian process. While this is a neat coincidence, it’s not especially surprising given an abundance of work on relating neural networks and Gaussian processes as two leading forms of universal function approximators. However, the part that interested me the most was in their experiemntal section in which they discuss using the deep image prior for reconstruction as well as other image processing tasks and use Langevin dynamics to draw samples of $\theta$ leading to a posterior distribution of $p(x \vert \tilde{x})=\int_\theta p(x\vert \theta,\tilde{x})p(\theta \vert \tilde{x})d\theta$. Note that in this framework, there’s no mention of distributions over $z$ or $\tilde{z}$ - these are treated as fixed inputs!
I do want to take a minute here to critique the authors’ description, though. They aren’t using stochastic gradient Langevin Dynamics (SGLD) in the way that most people understand it. Let’s take a look at the deep image prior’s weight update equation from section 4 of this paper:
\[\eta_t \sim N(0,\epsilon)\\
\theta_{t+1}=\theta_t +\frac{\epsilon}{2}[\underbrace{\nabla_\theta \log p_\theta(\tilde{x}\vert\theta)}_{\substack{\text{Reconstruction error}\\ \text{for non-masked data}}}
+\overbrace{\nabla_\theta p(\theta)]}^{\text{DIP}}+\eta_t\\\]
The “Langevin” part comes about because the behavior of $\theta$ can be thought of as a particle subject to random perturbations (i.e. the isotropic noise $\eta_t$) while also under the influence of a force represented as the gradient of a potential. In this context, the gradient is the sum of a gradient due to reconstruction error and due to the deep image prior (DIP). The “stochastic” part of SGLD refers to using minibatch approximations for the gradient estimator which we are forced to do because a full batch would be too computationally expensive. However, here, note that $\tilde{x}$ isn’t a minibatch - it’s the entire dataset! Within the setup laid out by Cheng et al., the deep generative model $f_\theta$ has parameters $\theta$ which do indeed need to be optimized, but they are only optimized using a single partial image $\tilde{x}$ rather than multiple images $x_1,…,x_N$ as is done with standard VAE and GAN training protocols. Thus, they are really just implementing Langevin dynamics. This is the same thing as MALA with the Metropolis accept/reject step removed.
Since only a single image is used to optimize / sample $\theta$, the model is really only able to capture information from two sources: (1) the inductive bias baked into the deep image prior (i.e. strong spatial covariance in the GP interpretation) and (2) image structures present in $\tilde{x}$ which thus influence $p(x\vert \tilde{x})$). This could have serious downsides - suppose we’d like to compute a posterior distribution of completions for an image of a man with blond hair yet his mouth (and mustache) are cropped out. Since the single image does not have any brown hair in it, it is unlikely that the deep image prior can be used to generate image completions consistent with a brown mustache. Yet, it is possible that in the collection of all training images $x_1,…,x_N$ there exist some pictures of men with blond hair and a brown mustache. This sort of outcome is also unlikely to have a nonnegligible probability under the deep image prior. All in all, this paper raises a number of possible directions for UQ with structured data via Langevin MCMC and also obviates the need to do any training at all!
Strictly speaking, this paper has nothing to do with image completion and it is focused entirely about treating neural network weights as random variables rather than fixed parameters. However, it’s not hard to see how this might give a possible receipe for posterior inpainting. Suppose we have a procedure $\nu (\theta,\tilde{x})$ that takes in a set of neural network weight parameters $\theta$ as well as a partially completed image $\tilde{x}$ and deterministically returns an estimated completion $\hat{x}$. For example, see [Yeh et al. (2017)](arxiv.org ‘ cs
Semantic Image Inpainting with Deep Generative Models) for such a recipe. Then, if we could sample from a posterior distribution $p(\theta\vert \mathcal{D})$ then we could perform ancestral sampling to approximate $p(\hat{x}\vert\mathcal{D})=\int_\theta p(\hat{x}\vert\theta)p(\theta\vert\mathcal{D})d\theta$. Since this paper is about providing $p(\theta\vert\mathcal{D})$, I judge it as highly relevant to the task at hand. The paper works with a similar conceptual framework as the Autoencoding Variational Bayes paper but targets the neural network weights $\theta$ instead of the latent variables $z$ for a variational approximation. I’m going to spend much more time analyzing this paper because I think it provides a really nice template for thinking about Bayesian deep learning.
The stated objective in this work is to pose neural network training as solving the following optimization problem for the variational free energy $\mathcal{F}$ in terms of the variational parameters $\phi$ given dataset $\mathcal{D}$, likelihood $p(\mathcal{D}\vert\theta)$ and weight $p(\theta)$.
\(\begin{align}
\phi^* &=\underset{\phi}{\text{arg min }}\mathcal{F}(\mathcal{D},\theta,\phi)\\
&=\underset{\phi}{\text{arg min }}KL(q(\theta\vert\phi)\vert\vert p(\theta\vert\mathcal{D}))\\
&= \underset{\phi}{\text{arg min }}KL(q(\theta\vert\phi)\vert\vert p(\theta)) - E_{q(\theta\vert\phi)}\left[\log p(\mathcal{D}\vert \theta)\right]
\end{align}\)
If this notation is opaque or these equations are especially hard to follow, I recommend looking at my earlier post which repeats these calculations ad nauseum. In line with their derivation, we next define the variational free energy as \(\mathcal{F}(\theta,\phi)=KL(q(\theta\vert\phi)\vert\vert p(\theta)) - E_{q(\theta\vert\phi)}\left[\log p(\mathcal{D}\vert \theta)\right]\) and then attempt to find a Monte Carlo estimator of its gradient $\nabla_\phi \mathcal{F}(\theta,\phi)$. Unfortunately, this has the form $\nabla_\phi E_{q(\theta\vert\phi)}\left[…\right]$ and we can’t push the gradient operator inside the expectation since the density that we are integrating against itself depends on $\phi$. To solve this, we make use of the reparameterization trick and a deterministic function $t (\epsilon,\phi)$to rewrite $\theta=t(\epsilon,\phi)$. This yields:
\[\begin{align}
\nabla_\phi \mathcal{F}(\theta,\phi)&=\nabla_\phi E_{q(\theta\vert\phi)}\left[\log\frac{q(\theta\vert\phi)}{p(\theta)}-\log p(\mathcal{D}\vert \theta)\right]\\
&=\nabla_\phi E_{q(\theta\vert\phi)}\left[\log q(\theta\vert\phi) - \log p(\theta)-\log p(\mathcal{D}\vert \theta)\right]\\
&=\nabla_\phi E_{p(\epsilon)}\left[\log q(t\vert\phi) - \log p(\theta)-\log p(\mathcal{D}\vert \theta)\right]\\
\end{align}\]
At this point we simplify the notation by designating \(f(\theta,\phi) = \log q(\theta\vert\phi) - \log p(\theta)-\log p(\mathcal{D}\vert \theta)\), leading to the following:
\(\begin{align}
\nabla_\phi \mathcal{F}(\theta,\phi)&=\nabla_\phi E_{p(\epsilon)}\left[f(t,\phi)\right]\\
&= E_{p(\epsilon)}\left[\nabla_\phi f(t,\phi)\right]\\
\end{align}\)
To avoid having to specify in terms of products, I’ll focus on the elementwise derivative as done in the paper:
\(\begin{align}
\frac{\partial}{\partial\phi}\mathcal{F}(\theta,\phi)
&= E_{p(\epsilon)}\left[\frac{\partial}{\partial\phi} f(t,\phi)\right]\\
&= E_{p(\epsilon)}\left[\frac{\partial f}{\partial\theta}\frac{\partial \theta}{\partial\phi} + \frac{\partial f}{\partial \phi}\right]\\
\end{align}\)
It turns out that this step is really all you need to be able to implement a BBB estimation scheme in a modern deep learning framework, though. See here for a great example from the Gluon developers! We will need to make some more assumptions about the specific parametric form of $t(\phi,\epsilon)$ to make the above gradient more explicit. While we’re free to consider any transformation $t: \epsilon\rightarrow\theta$, one of the simplest is a scale-location transformation where the $i$-th neural network weight is written as $\theta_i = \mu_i + \epsilon_i \cdot \sigma_i$ with $\mu_i$ giving the variational posterior mean of $\theta_i$ and $\sigma_i$ providing the variational posterior standard deviation. The standard deviation is always positive and we’d prefer to perform unconstrained optimization when possible, so Blundell et al. reparameterize $\sigma_i=\log (1+e^{\rho})$ instead.
Since the vector $\phi$ is supposed to include all of the variational parameters and each element of $\theta$ has a variational mean and standard deviation, the vector $\phi$ is going to have double the dimension of $\theta$. Let’s split apart $\phi$ and examine some of the gradients more closely, focusing on the variational mean $\mu$:
\[\begin{align}
\frac{\partial\mathcal{F}}
{\partial\mu}
&=E_{p(\epsilon)}\left[\frac{\partial f}{\partial\theta}\cdot\frac{\partial\theta}{\partial\mu}+\frac{\partial{f}}{\partial\mu}\right]\\
&=E_{p(\epsilon)}\left[\frac{\partial}{\partial\theta}\left[\log q(\theta\vert\phi)-\log p(\theta)-\log p(\mathcal{D}\vert\theta)\right]\cdot\frac{\partial\theta}{\partial\mu}+\frac{\partial{f}}{\partial\mu}\right]
\end{align}\]
Addressing each of these terms within $\partial f/\partial \mu$ individually will be more enlightening. The form of the conditional variational density $q(\theta\vert\phi)$ depends on our model assumptions; the default version given in Blundell et al. assumes a multivariate normal with diagonal covariance. Thus, we have \(\log q(\theta\vert\phi)\propto \frac{1}{2}(\theta-\mu)^T\Sigma_q^{-1}(\theta-\mu)\). Here, the covariance matrix $\Sigma_q$ has the variances $\sigma_i^2$ on its diagonal, so its inverse will also be diagonal with diagonal entries of $1/\sigma_i^2$. We can see that this is going to push the values of $\mu$ in line with the values of $\theta$.
Next, the prior $p(\theta)$ is going to play a regularization role. We have a couple of options here; using an isotropic Gaussian with sufficiently small variance will induce $L_2$ regularization on the weights with equal strength everywhere. The study authors point out that a prior which allows for some large coefficients but mostly small coefficients can be useful and thereby include a two-component mixture of Gaussians with the idea that one mixture has a small variance (preferring lots of coefficients with small values) and the other mixture has a large variance to allow for large coefficient values to occasionally pop up. The mixture weights would need to be estimated, however, and Blundell et al. simply leave that up to your favorite choice of hyperparameter tuning.
Finally, the log-likelihood $p(\mathcal{D}\vert\theta)$ is straightforward to understand - it’s the error resulting from the mismatch between predictions $\hat{x}$ and true values $x$. In the case of a Gaussian likelihood, we get square error loss and for a Laplace likelihood, we recover absolute error loss.
For all of the terms in $\partial f/\partial \theta$, the gradients come down to gradients of quadratic forms of some type and under the right prior assumptions can even be done analytically.
Back in equation (12), the next term \(\partial \theta/\partial\mu\) is just $1$ since $\theta \propto \mu$ in our function \(\theta=t(\phi,\epsilon)=t(\mu,\rho,\epsilon)\). Then, the final term \(\frac{\partial f}{\partial \mu}\) is much like the first term, except the parts that don’t depend on $\mu$ will drop out. Again, I want to stress that none of these calculations need to be done by hand - autodif software like Torch or Tensorflow will do these automatically. Once $\partial{\mathcal{F}}/\partial \mu$ is calculated with the above steps, it’s easy to apply stochastic gradient descent with a Monte Carlo estimator of $\partial \mathcal{F}/\partial \mu$ in order to do training. A similar recipe can be followed for the scale parameter $\rho$.
Treating the network weights $\theta$ as the random variable is orthogonal in some sense to the methods which treat the latent variable $z$ as the random quantity to be optimized over. Including both sources of uncertainty could be a promising line of future research.
]]>